Your Name: _______________________ PHY203

Exam #3

Chapters 8-10

Fri., 4/11/08

Solutions

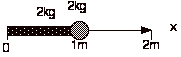
1. Masses are placed as follows: 2kg at x=1m and a 2kg rod 1m in length placed along the x-axis from x=0 to x=1m, as shown above. Find the center of mass:

a. 0.25m x_cm=[(2kg)(1m) + (2kg)(0.5m)]/(4kg)

b. 0.5m

c. 0.75m

d. 0.67m

e.1.0m

2. A 10kg duck is flying North at 5m/s. A second duck of mass 5kg is flying South at 10m/s. Find the velocity of the center of mass:

a. 0 m/s v_cm=[(10kg)(5m/s) - (5kg)(10m/s)]/(15kg) = 0

b. 0.33 m/s

c. 1.0 m/s

d. 5.0 m/s

e. none of the above

3. A particle of mass 5kg is traveling in a circle of radius 3m at a speed of 2.5m/s. Find the magnitude of the angular momentum:

a. 10.0 kgm²/s L=r x p = (3m)(5kg)(2.5m/s)

b. 12.5 kgm²/s

c. 37.5 kgm²/s

d. 112.5 kgm²/s

e. none of the above

For problems 4 and 5:

A solid disk of mass 2kg and radius 0.5m is rotating with an angular speed of 5rad/s.

4. Find the moment of inertia about the center:

a. 0.25 kgm² I= 1/2mr² = 1/2(2kg)(0.5m)²

b. 0.5 kgm²

c. 1.25 kgm²

d. 2.5 kgm²

e. none of the above

5. Find the magnitude of the angular momentum:

a. 0.25 kgm²/s L=Iw = (0.25 kgm²)(5rad/s)

b. 0.5 kgm²/s

c. 1.25 kgm²/s

d. 2.5 kgm²/s

e. none of the above

6. Let the vector A = 5i – 4j and B = 3j. Find the vector C = A x B:

a. -15k C= (5i – 4j) x (3j) = 15(i x j) – 12(j x j) = 15k - 0

b. +15k

c. -12i - 15k

d. -12i + 15k

e. 12i - 15k

7. Albert Einstein stands on a platform with his arms extended and holding masses in each hand. The combined moment of inertia of him plus weights in this position is 12kgm². The platform is rotating with an angular speed of 5rad/s. If he brings his arms in towards his body, his moment of inertia drops to 8 kgm². Find his new angular speed:

a. 0.13 rad/s L=Iw; I₁w₁ = I₂w₂

b. 0.3 rad/s (12kgm²) (5rad/s) = (8 kgm²) (w₂)

c. 1.5 rad/s

d. 3.33 rad/s

e. 7.5 rad/s

8. A wheel is spun up from rest with a constant angular acceleration of a=3.5rad/s². Find the angular velocity after 15 sec.:

a. 4.3 rad/sec. w = w_o + at = 0 + (3.5rad/s²)(15)

b. 26.25 rad/sec.

c. 52.5 rad/sec.

d. 394 rad/sec.

e. none of the above

9. A disk of mass 10 kg and radius 0.5 m is at rest. A force of 10 N is applied at the

edge of the disk at an angle of 60^o as shown.

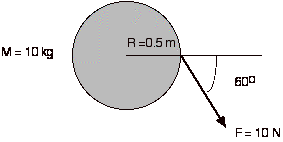
Find the magnitude of the torque, t.

a. 2.5 Nm t = rFsinq = (0.5m)(10N)(sin60^o)

b. 4.3 Nm

c. 5.0 Nm

d. 10.8 Nm

e. 12.5 Nm

10. Find the kinetic energy of a solid sphere with mass=2kg and radius=1m which is rolling without slipping with a center-of-mass velocity of 5 m/s:

a. 7.0 J K=(1/2)mv² + (1/2)Iw² = =(1/2)mv² + (1/2)(2/5)mr²(v/r)²

b. 25 J = (1/2 + 1/5)mv² = (7/10)(2kg)(5m/s)²

c. 35 J

d. 37.5 J

e. 50J

11. A 5.0kg block is traveling in the positive x-direction on a horizontal, frictionless

surface at an initial speed of 8.0m/s. The block explodes and breaks into two

pieces. One piece (m₁ = 3.0kg) shoots off in the negative y direction with a speed

of 4.0m/s.

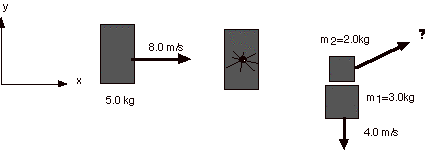
a. Using the coordinate system shown above, calculate the initial momentum

and kinetic energy of the block before the explosion. Write the momentum in vector

notation.

p_i = (5kg)(8m/si) = 40kgm/si

K_i=(1/2)mv² = 1/2(5kg)(8m/s)² = 160J

b. Find the momentum of the combined two-block system just after the explosion

and write the momentum in vector notation.?

same; p_f = 40kgm/si

c. Find the velocity of the second block ( m₂) after the explosion and write it in vector notation.

p_f = 40kgm/si = (3kg)(-4m/sj) + (2kg)( v_2xi + v_2yj )

x: 40kgm/s = (2kg)( v_2x); v_2x = 20m/s

y: 0 = (3kg)(-4m/s) + (2kg)( v_2y); v_2y = 6m/s

v₂ = 20m/si + 6m/sj

d. Is the process elastic or inelastic? Prove it quantitatively.

K_f=(1/2)mv² = 1/2(3kg)(4m/s)² + 1/2(2kg)[(20m/s)² + (6m/s)² ] = 460J

K_i not = K_f so inelastic